考完研,数学考得好烂,受数学老师指导,去图书馆借了几本数学书看看,在此记一下重点~
《微积分五讲》 是华罗庚的弟子,龚昇先生所著,薄薄的一个小本,看完有一种高维打击的感觉
龚昇:数学中每一步真正的进展都与更有利的工具和更简单的方法的发现密切联系者,这些工具和方法同时会有助于理解已有的理论并把陈旧的、复杂的东西抛到一边。数学科学发展的这种特点是根深蒂固的。
数学课程结构
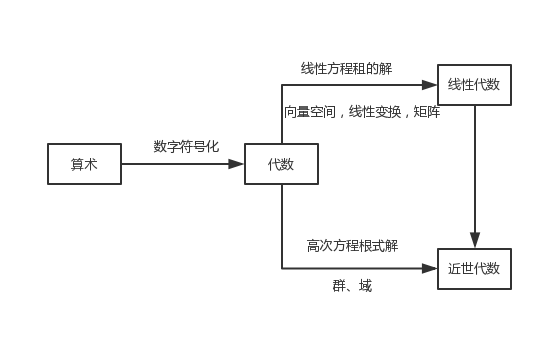
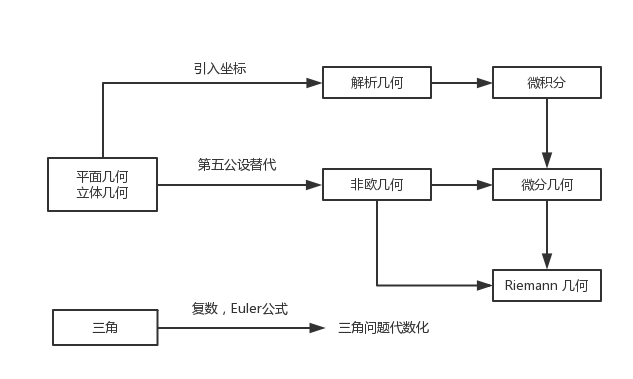
微积分的主要矛盾
微积分这门学科中,主要矛盾是微分和积分的矛盾。
微积分这门学科的内容是由三部分组成,即微分、积分、指出微分和积分是一对矛盾的微积分基本定理这三个部分所组成。
此处略过牛来公式,格林,高斯,斯托克斯公式等相关内容。。。。
重点:外微分形式
要讲外微分形式,必须先讲定向的概念,法国著名的拓扑学家托姆(R. Thom,1923~2002)教授,曾对吴文俊教授表达过这样的意见:定向概念是几何拓扑中最有深刻意义的伟大创造之一。
满足下述两条规则的微分乘积称为微分的外乘积:
\[\begin{gather} \mathrm dx \wedge \mathrm dx = 0 \\ \mathrm dx \wedge \mathrm dy=- \mathrm dy\wedge \mathrm dx \end{gather}\]由微分的外乘积乘上函数组成的微分形式,称为外微分形式.
若P,Q,R,A,B,C,H都是x,y,z的函数,则\(P\mathrm dx + Q\mathrm dy + R\mathrm dz\)为一次外微分形式(由于一次没有外乘积,所以与普通的微分形式是一样的);
Adx Λ dy + Bdy Λ dz + Cdz Λ dx
为二次外微分形式;
Hdx Λ dy Λ dz
为三次外微分形式;
把P,Q,R,A,B,C,H等称为外微分形式的系数,而称函数f为0次外微分形式。
外微分的外乘积满足分配律及结合律,及如果λ,μ,ν是任意三个外微分形式,则
(1) (λ + μ) Λ ν = λ Λ ν + μ Λ ν
λ Λ (μ + ν) = λ Λ μ + λ Λ ν
(2) λ Λ (μ Λ ν) = (λ Λ μ) Λ ν
当然,外微分形式的乘积不满足交换律,而满足
(3) 若λ为p次外微分形式,μ为q次外微分形式,则
\[\mu \wedge \lambda =\left( -1\right) ^{pq}\lambda \wedge \mu\]对于外微分形式ω,可以定义外微分算子如下:
对于零次外微分形式,即函数\(f\),定义
\[\mathrm df=\dfrac {\partial f}{\partial x}\mathrm dx+\dfrac {\partial f}{\partial y}\mathrm dy + \dfrac {\partial f}{\partial z}\mathrm dz\]即是普通的全微分算子。
对于一次外微分形式
\[\omega = P\mathrm dx + Q\mathrm dy + R\mathrm dz\]定义
\[\mathrm d\omega = \mathrm dP \wedge \mathrm dx + \mathrm dQ \wedge \mathrm dy + \mathrm dR \wedge \mathrm dz\]即对P, Q,R进行外微分,然后进行外乘积,由于
\[\mathrm dP=\dfrac {\partial P}{\partial x}\mathrm dx+\dfrac {\partial P}{\partial y}\mathrm dy + \dfrac {\partial P}{\partial z}\mathrm dz\] \[\mathrm dQ=\dfrac {\partial Q}{\partial x}\mathrm dx+\dfrac {\partial Q}{\partial y}\mathrm dy + \dfrac {\partial Q}{\partial z}\mathrm dz\] \[\mathrm dR=\dfrac {\partial R}{\partial x}\mathrm dx+\dfrac {\partial R}{\partial y}\mathrm dy + \dfrac {\partial R}{\partial z}\mathrm dz\]所以
\[\mathrm d\omega = (\dfrac {\partial P}{\partial x}\mathrm dx+\dfrac {\partial P}{\partial y}\mathrm dy + \dfrac {\partial P}{\partial z}\mathrm dz) \wedge \mathrm dx + (\dfrac {\partial Q}{\partial x}\mathrm dx+\dfrac {\partial Q}{\partial y}\mathrm dy + \dfrac {\partial Q}{\partial z}\mathrm dz) \wedge \mathrm dy +(\dfrac {\partial R}{\partial x}\mathrm dx+\dfrac {\partial R}{\partial y}\mathrm dy + \dfrac {\partial R}{\partial z}\mathrm dz) \wedge \mathrm dz\]经过整理,得到
\[\mathrm d\omega = (\dfrac {\partial R}{\partial y}-\dfrac {\partial Q}{\partial z}) \mathrm dy \wedge \mathrm dz + (\dfrac {\partial P}{\partial z}-\dfrac {\partial R}{\partial x}) \mathrm dz \wedge \mathrm dx +(\dfrac {\partial Q}{\partial x}-\dfrac {\partial P}{\partial y}) \mathrm dx \wedge \mathrm dy\]以此类推。。 显然我们可知,在三维空间中,任意三次外微分形式的外微分为零。
在三维Euclid空间,Green公式、Stokes公式与Gauss公式实际上都是可以由同一公式写出来,这个定理(或公式)也叫做斯托克斯(Stokes)定理(Stokes公式):
\[\int_{\partial \Omega} \omega = \int_\Omega \mathrm d \omega\]这里,\(\omega\)为外微分形式,\(\mathrm d\omega\) 为\(\omega\)的外微分,\(\Omega\)为\(\mathrm d\omega\)的积分区域,\({\partial \Omega}\)表示\(\Omega\)的边界,\(\Omega\)的维数与\(\mathrm d\omega\)的次数相一致,\(\int\)表示区域有多少维数就是多少重数。
从这里还可以看出:除了Green公式Stokes公式以及Gauss公式以外,在三维Euclid空间中,联系区域与边界的积分公式不会再有了,因为这是三次外微分形式为零。
| 外微分形式的次数 | 空间 | 公式 |
|---|---|---|
| 0 | 直线段 | Newton-Leibniz公式 |
| 1 | 平面区域 | Green公式 |
| 1 | 空间曲面 | Stokes公式 |
| 2 | 空间中区域 | Gauss公式 |
斯托克斯公式揭露了在三维Euclid空间中微分与积分是如何成为一对矛盾的,这对矛盾的一方为外微分形式,另一方为线积分、面积分、体积分。Stokes公式是微积分中具有本质性的定理,是微积分这门学科的一个顶峰,它使微积分从古典走向现代,是数学中少有的简洁、美丽而深刻的定理之一。
从外微分形式的观点,在三维Euclid空间中,有且只能有三个度,即梯度、旋度、散度。
除此之外,还有离散与连续、局部与整体、有限与无限、数与形、特殊与一般等,这些矛盾几乎在数学的所有分支中都起着重要的左右,在微积分这门学科中当然也是这样。
以上所有内容全部摘自龚昇先生的《微积分五讲》,仅做个人记录,并测试latex之用(敲latex真的好费劲!),有兴趣的同学可以去找书看。